Schinckel.net

There is a mathematical problem called the Eight Queens problem, which one of my teachers mentioned in passing in a Lecture the other day. I was mainly surprised as I hadn’t heard of it before.

The theory is thus. Imagine you have an 8x8 chessboard, and 8 queens. Is it possible to place each queen on the chessboard so that it cannot be taken by (and therefore not take) any other queen?

Graham mentioned it was interesting to do with a recursive method.

I thought it was something that was a good candidate for Logic Programming.

To begin with, I broke the problem down a little. For instance, there is one unique and trivial solution with a 1x1 chessboard and one queen.

With a 4x4 chessboard, there are two solutions that are just mirrors of one another, one of which I found almost immediately by just thinking about it:

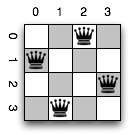
Notice here that as long as you do not put the first queen in a corner, you will get a solution.

Doing this gave me some thoughts as to how to automate the process. Each queen has an X and a Y coordinate, and in each case, every queen must have a unique X coordinate, and a unique Y coordinate. This prevents them being on the same row or column as another queen.

Then, some quick calculations showed that in each of these cases, the difference of the X and Y coordinates is unique also. This prevents them appearing on the same down-right diagonal. Note here that not every diagonal has a queen on it - in fact, only one more than half of the possible number of diagonals does.

Further along the same lines of thought, we need a way to test if they appear on the same down-left diagonal. Some further calculations showed this is given by the sum of the X and Y coordinates.

So, we have four simple rules for determining if a queen can take another queen.

In my prolog solution, I call this unsafe/2.

    unsafe([X1,Y1],[X2,Y2]) :-
        X1 = X2;
        Y1 = Y2;
        X1 is Y1 + X2 - Y2;
        X1 is (X2 + Y2) - Y1.

We can then reverse this rule to find a safe pair:

    safe(A,B) :- \\+unsafe(A,B).  

To find if a set of queens are all safe together, we have a nice recursive predicate, queens/1:

    queens([_]).  
    queens([Q1, Q2|Qlist]) :-
        safe(Q1, Q2),
        queens([Q1|Qlist]),
        queens([Q2|Qlist]).

All that we need now is a method of generating permutations, and we are done. I’ll not post my perm/2 solution, since it is widely known.

    queens8([[1,A],[2,B],[3,C],[4,D],[5,E],[6,F],[7,G],[8,H]]) :-
        perm([1,2,3,4,5,6,7,8],[A,B,C,D,E,F,G,H]),
        queens([[1,A],[2,B],[3,C],[4,D],[5,E],[6,F],[7,G],[8,H]]).

Calling queens8(X) will return every possible combination that fulfils the requirements of the Eight Queens problem. There are 92, but these are not all rotation- and reflection-unique.

One solution is shown below.

This is not the first solution I found, just a nice one :)

The only thing I haven’t yet figured out is how to automate the extension of this to any size board. At the moment I also have a queens4, queens5, and so on set of predicates. It would be nice to generalise this to queens(N,X). It would also be kind of cool to show the number of solutions, rather than each solution. And a clever way to show only rotation- or reflection-unique solutions would be even better.